การแยกตัวประกอบ

ตัวประกอบ ของจำนวนใดจำนวนหนึ่งคือ ค่าใดก็ตามที่เมื่อนำมาคูณกันแล้วได้ผลลัพธ์เท่ากับจำนวนนั้น หรือกล่าวได้ว่า จำนวนไม่ว่าจะเป็นจำนวนใดก็ตาม ล้วนมีค่าเท่ากับผลคูณของตัวประกอบของจำนวนนั้นทั้งหมด ดังนั้นการแยกตัวประกอบก็คือ การนำจำนวนใดจำนวนหนึ่งมาเขียนให้อยู่ในรูปของจำนวนสองจำนวนคูณกัน หรือมากกว่าสองจำนวนคูณกัน  อ่านเพิ่มเติม

โดเมนและเรนจ์

โดเมนและเรนจ์ของความสัมพันธ์ เป็นรากฐานสำคัญที่จะนำเข้าสู่เรื่องของการสร้างกราฟของความสัมพันธ์อีกทั้งการวิเคราะห์ฟังก์ชัน……นิยาม   ถ้ากำหนดให้  r  เป็นความสัมพันธ์
…..โดเมนของ  r  คือ  เซตของ อ่านเพิ่มเติม

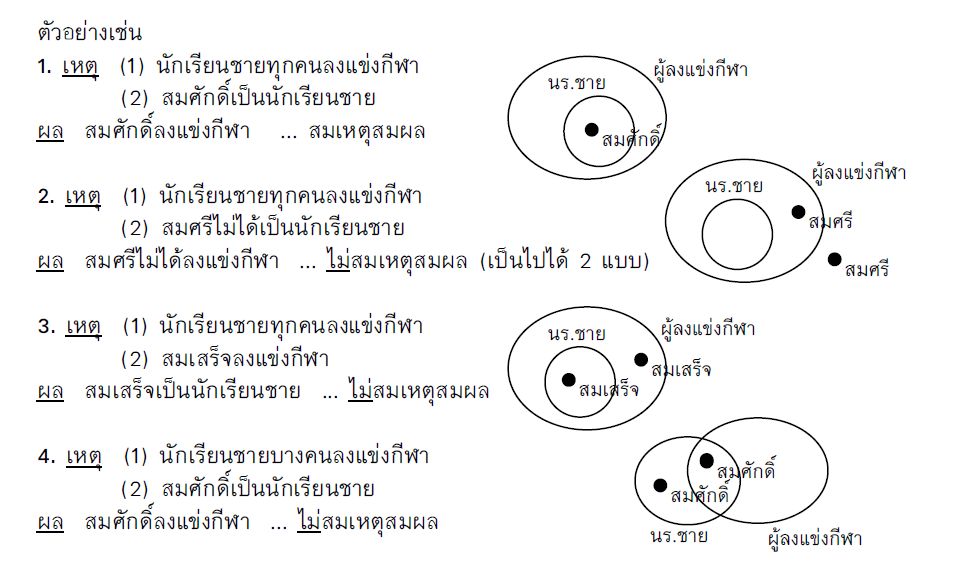
การให้เหตุผลแบบนิรนัย

การให้เหตุผลแบบนิรนัยเป็นการนำความรู้พื้นฐานซึ่งอาจเป็นความเชื่อ ข้อตกลง กฎ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อน และยอมรับว่าเป็นความจริงเพื่อหาเหตุผลนำไปสู่ข้อสรุป เป็นการอ้างเหตุผลที่มีข้อสรุปตามเนื้อหาสาระที่อยู่ภายในขอบเขตของข้ออ้างที่กำหนด อ่านเพิ่มเติม

การให้เหตุผลแบบอุปนัย

การให้เหตุผลแบบอุปนัย (Inductive Reasoning) เกิดจากการที่มีสมมติฐานกรณีเฉพาะ หรือเหตุย่อยหลายๆ เหตุ เหตุย่อยแต่ละเหตุเป็นอิสระจากกัน มีความสำคัญเท่าๆ กัน และเหตุทั้งหลายเหล่านี้ไม่มีเหตุใดเหตุหนึ่งแสดงให้เห็นถึงความเป็นสมมติฐานกรณีทั่วไป หรือกล่าวได้ว่า การให้เหตุผลแบบอุปนัยคือการนำเหตุย่อยๆ แต่ละเหตุมารวมกัน เพื่อนำไปสู่ผลสรุปเป็นกรณีทั่วไป เช่นตัวอย่างการให้เหตุผลแบบอุปนัย  อ่านเพิ่มเติม

จำนวนจริง

จำนวนจริง

เซตของจำนวนจริงประกอบด้วยสับเซตที่สำคัญ  ได้แก่

- เซตของจำนวนนับ/ เซตของจำนวนเต็มบวก เขียนแทนด้วย  I  อ่านเพิ่มเติม

เพาเวอร์เซต

เพาเวอร์เซต (Power Set)

คำว่า เพาเวอร์เซต เป็นคำศัพท์เฉพาะ ซึ่งใช้เป็นชื่อเรียกเซตเซตหนึ่งที่เกี่ยวข้องกับเรื่องสับเซต

เพาเวอร์เซตของ A เขียนแทนด้วย P(A)

P(A) คือเซตที่มีสับเซตทั้งหมดของ A เป็นสมาชิก อ่านเพิ่มเติม

สับเซต

สับเซต (Subset)

ถ้าสมาชิกทุกตัวของ A เป็นสมาชิกของ B แล้ว จะเรียกว่า A เป็นสับเซตของ B จะเขียนว่า
เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B

ถ้าสมาชิกบางตัวของ A ไม่เป็นสมาชิกของ B จะเรียกว่า A ไม่เป็นสับเซตของ B
เซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B อ่านเพิ่มเติม